This page is associated with the monograph
Uniformization of embedded surfaces
by Neil Strickland, and the related Maple code.
Let $X\subset S^3$ be a smoothly embedded closed surface of genus $g\gt 1$. As we will explain, $X$ automatically has a very rich and rigid geometric structure. Indeed, $X$ inherits a Riemannian metric from $S^3$, and after specifying some conventions we also obtain a well-defined orientation. Now consider a point $x\in X$, and let $T_xX$ denote the corresponding tangent space. Let $J_x\colon T_xX\to T_xX$ be the anticlockwise rotation through $\pi/2$ (which is meaningful given the metric and orientation). This depends smoothly on $x$ and satisfies $J_x^2=-1$, so it gives an almost complex structure on $X$. It has been known since the early twentieth century that any almost complex structure on a manifold of real dimension two integrates to give a genuine complex structure. Thus, $X$ can be regarded as a compact Riemann surface. It is known that any compact Riemann surface can be regarded as a projective algebraic variety over $\mathbb{C}$, and also as a branched cover of the Riemann sphere. Alternatively, as we have assumed that the genus is larger than one, the universal cover of $X$ is conformally equivalent to the open unit disc $\Delta$. This means that $X$ is conformally equivalent to the quotient $\Delta/\Pi$ for some Fuchsian group $\Pi$.
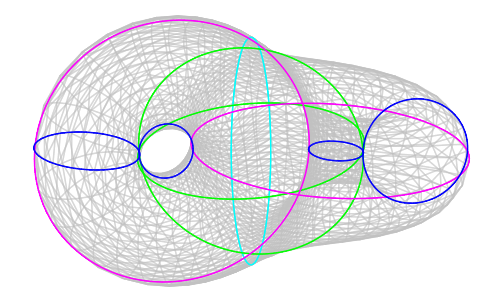
To the best of our knowledge, the literature contains no examples where a significant fraction of this structure can be made explicit. This project is a partially successful attempt to provide such an example, involving the surface \[ EX^* = \{x\in S^3\; | \; (3x_3^2-2)x_4+\sqrt{2}(x_1^2-x_2^2)x_3=0 \} \]
by Neil Strickland, and the related Maple code.
Let $X\subset S^3$ be a smoothly embedded closed surface of genus $g\gt 1$. As we will explain, $X$ automatically has a very rich and rigid geometric structure. Indeed, $X$ inherits a Riemannian metric from $S^3$, and after specifying some conventions we also obtain a well-defined orientation. Now consider a point $x\in X$, and let $T_xX$ denote the corresponding tangent space. Let $J_x\colon T_xX\to T_xX$ be the anticlockwise rotation through $\pi/2$ (which is meaningful given the metric and orientation). This depends smoothly on $x$ and satisfies $J_x^2=-1$, so it gives an almost complex structure on $X$. It has been known since the early twentieth century that any almost complex structure on a manifold of real dimension two integrates to give a genuine complex structure. Thus, $X$ can be regarded as a compact Riemann surface. It is known that any compact Riemann surface can be regarded as a projective algebraic variety over $\mathbb{C}$, and also as a branched cover of the Riemann sphere. Alternatively, as we have assumed that the genus is larger than one, the universal cover of $X$ is conformally equivalent to the open unit disc $\Delta$. This means that $X$ is conformally equivalent to the quotient $\Delta/\Pi$ for some Fuchsian group $\Pi$.
To the best of our knowledge, the literature contains no examples where a significant fraction of this structure can be made explicit. This project is a partially successful attempt to provide such an example, involving the surface \[ EX^* = \{x\in S^3\; | \; (3x_3^2-2)x_4+\sqrt{2}(x_1^2-x_2^2)x_3=0 \} \]

- The monograph itself is on the arxiv and also
here.
- There is also a large body of related
Maple
code and worksheets, together with graphics and data files
produced by that code.
- The arxiv page also has the code and worksheet files, uploaded as ancilliary files with the main LaTeX document. However, readers may find it more convenient to use this page instead of the arxiv page.
- As well as the discussion of the Maple code structure in the memoir,
there are some documentation files:
- Index of classes
- Index of definitions (in non object oriented code)
- Index of images
- The code and worksheets can be downloaded as a .zip file or as a .tgz file. These files contain only a few of the graphics generated by the code, and none of the data files. To start using the code, one should open the file genus2.mw in the worksheets directory.
- Alternatively, the above files can be obtained from the GitHub repository.
- One can also download much larger files containing all graphics and data as well as the code, in .zip format (300MB) or .tgz format (190MB).